¿Qué es el contradominio en matemáticas? - Explora el rango completo de una función
En matemáticas, el contradominio se refiere al conjunto de todos los posibles valores de salida o resultados que una función matemática puede generar a partir de un conjunto dado de valores de entrada.
Es esencialmente el rango de valores que la función puede tomar como resultado. El contradominio tiene un papel muy importante y crucial en la comprensión y el análisis de las funciones, ya que permite definir claramente el alcance de las soluciones posibles en un contexto matemático específico.
Importancia del contradominio en matemáticas
El contradominio en matemáticas desempeña un papel de vital importancia en el análisis y la comprensión de las funciones. Este concepto se refiere al conjunto de posibles valores de salida que una función matemática puede generar a partir de un conjunto dado de valores de entrada.
En otras palabras, el contradominio establece los límites y las posibilidades de resultados que una función puede arrojar. Esta noción es esencial para delinear con precisión el comportamiento de una función y permite a los matemáticos comprender qué valores pueden tomar las variables dependientes en relación con las variables independientes.
Además, el contradominio facilita la identificación de relaciones y patrones en los datos y contribuye a la resolución de problemas en una variedad de campos, desde la física hasta la economía. Por ejemplo, en estadísticas, el conocimiento del contradominio es esencial para determinar la distribución de probabilidad de una variable aleatoria y calcular la probabilidad de eventos específicos.
El contradominio en matemáticas no solo es una herramienta fundamental para el análisis y la modelización, sino que también juega un papel esencial en la resolución de problemas prácticos y en la toma de decisiones basadas en datos en numerosos campos de estudio y aplicaciones.
¿Qué es dominio y contradominio en matemáticas
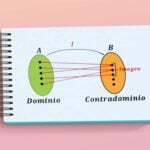
En matemáticas, el dominio y el contradominio son conceptos esenciales que se utilizan para definir y comprender las funciones. El dominio de una función se refiere al conjunto de todos los valores de entrada variables independientes para los cuales la función está definida, y puede producir un resultado válido.
En otras palabras, representa las entradas permitidas para la función. Por otro lado, el contradominio, también conocido como 'codominio', se refiere al conjunto de todos los posibles valores de salida variables dependientes que la función puede generar a partir de su dominio.
El contradominio establece los límites y las posibilidades de resultados que una función puede arrojar, y es esencial para entender cómo la función relaciona las entradas con las salidas. Estos conceptos son fundamentales en el análisis matemático y son la base para estudiar el comportamiento de las funciones en diversos campos, como la física, la economía, la ingeniería y un elemento en la estadística.
Al comprender y definir claramente el dominio y el contradominio de una función, los matemáticos pueden modelar fenómenos del mundo real, resolver problemas complejos y tomar decisiones basadas en datos con mayor precisión.
Es así como el dominio y el contradominio son pilares esenciales en la formulación y comprensión de funciones matemáticas, lo que los convierte en conceptos cruciales en la resolución de problemas.
Relación entre el contradominio y el rango de una función
La relación entre el contradominio y el rango de una función es un aspecto clave en el análisis matemático que arroja luz sobre cómo una función relaciona sus entradas con sus salidas. El contradominio, también conocido como 'codominio', representa el conjunto matemático de todos los posibles valores de salida que una función puede generar a partir de su dominio, es decir, las salidas potenciales.
Por otro lado, el rango de una función se refiere al conjunto de valores de salida que la función realmente produce cuando se evalúa en su dominio, es decir, las salidas reales. La relación entre ambos conceptos radica en que el rango de la función debe ser un subconjunto del contradominio.
En otras palabras, el rango está contenido dentro del contradominio, ya que una función no puede generar valores de salida que no estén previamente definidos en su contradominio como tal.
El rango proporciona una visión específica de las salidas reales de una función, mientras que el contradominio establece el conjunto más amplio de valores posibles. Al estudiar esta relación, los matemáticos pueden determinar si una función está utilizando completamente su contradominio o si existen limitaciones en su rango.
Esto es esencial para el análisis de funciones en diversas aplicaciones, desde la física hasta la ingeniería y la economía, ya que permite comprender con precisión cómo se relacionan las variables de entrada y de salida en un contexto particular.
Ejemplos de contradominio en matemáticas
El contradominio en matemáticas es un concepto relevante que se utiliza para comprender las funciones y sus posibles resultados. A continuación, se presentan algunos ejemplos de contradominio en distintos contextos matemáticos:
Las funciones trigonométricas como el seno y el coseno, el contradominio está relacionado con el rango de valores que estas funciones pueden tomar. Por ejemplo, el contradominio de la función seno es [-1, 1], ya que el valor del seno de un ángulo nunca supera 1 o desciende por debajo de -1. Esto significa que cualquier valor dentro de ese intervalo es un posible resultado de la función.
Las funciones lineales como y = mx + b, el contradominio puede ser todos los números reales o un subconjunto específico, dependiendo de las restricciones de la función. Si, por ejemplo, estamos modelando la temperatura en grados Celsius en función del tiempo en segundos, el contradominio sería el conjunto de todos los números reales, ya que la temperatura puede variar continuamente.
Las funciones discretas como funciones de conteo, el contradominio se compone de un conjunto finito de valores. Por ejemplo, si estamos contando la cantidad de estudiantes en una clase, el contradominio sería un conjunto de números naturales no negativos, ya que no puede haber un número fraccional o negativo de estudiantes.
Estos ejemplos ilustran cómo el contradominio se adapta a diferentes tipos de funciones y cómo es de suma importancia y esencial para definir claramente los posibles resultados que una función puede generar.